Exploding and Vanishing Gradients: On the difficulty of training Recurrent Neural Networks
Let’s assume we have a recurrent network with the following structure:
\[\begin{equation} \begin{aligned} \underbrace{\boldsymbol{x_t}}_{\text{d }} = \underbrace{ \boldsymbol{W}}_{\text{d,d}} \sigma (\boldsymbol{x_{t-1}}) + \boldsymbol{w_{in}} \boldsymbol{i_t } + \boldsymbol{b} \end{aligned} \end{equation}\]where x is a hidden state vector of some dimension d, and W is a square matrix of shape (d,d). $i_t$ is the input vector at time t, b is the bias vector, and $\sigma$ is some nonlinearity.
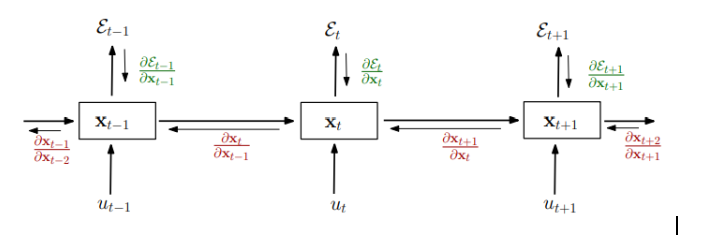
The derivative of vec $x_t$ in respect to vec $x_{t-1}$ is the Jacobian matrix, where $diag$ converts a vector into a diagonal matrix, and $\sigma ‘$ computes the derivative of σ in an element-wise fashion:
\[\begin{equation} \begin{aligned} \underbrace{ \frac{\partial \boldsymbol{x_t}}{\partial \boldsymbol{x_{t-1}}}}_{\text{d,d}} = \boldsymbol{W} diag(\sigma ' (\boldsymbol{x_{t-1}})) \end{aligned} \end{equation}\]Note that there is a mistake in the paper, and the W matrix in this formula should not be transposed. This is the reason: If you have a vector $y$ that depends on vector $x$ in the following manner: $y=Ax$ that means that $y_i = A_{ij} x_j$, therefore:
\[\begin{equation} \begin{aligned} (\frac{dy}{dx})_{ij} := \frac{dy_i}{dx_j} = \frac{d A_{ij}x_j}{dx_j} = A_{ij} \rightarrow \frac{dy}{dx} = A \end{aligned} \end{equation}\]The loss of a single time-step output is $\varepsilon_t$. The total loss, will be defined as the total losses of every individual time-steps: $ \varepsilon = \sum_{1 \leq t \leq T} \varepsilon_t $
Let’s denote $\theta$ as our model parameters we’re interested in. In this case $\theta$ can be the $W$ matrix. Let’s differentiate by $\theta$.
\[\begin{equation} \begin{aligned} \underbrace{ \frac{\partial \varepsilon }{\partial \theta} }_{\text{d,d}} = \sum_{1 \leq t \leq T} \frac{\partial \varepsilon_t }{\partial \theta} \end{aligned} \end{equation}\]Let’s explore the derivative of a $single$ time-step error, with respect to $\theta$.
For example let’s look at $ \varepsilon_3$. It is a function of $x_3$ only. $x_3$ is a function of both $\theta$, which is $W$ in our case and also a function of $x_2$, so we can write:
$\frac{d\varepsilon_3 }{d \theta} = \frac{\partial \varepsilon_3}{\partial x_3} \frac{dx_3 }{d \theta} = \frac{\partial \varepsilon_3}{\partial x_3} ( \frac{\partial x_3 }{\partial \theta} + \frac{dx_3 }{d x_2} ) $
Now, $x_2$ is also a function of $\theta$ and also $x_1$:
\[\begin{equation} \begin{aligned} \frac{dx_3 }{d x_2} = \frac{\partial x_3 }{\partial x_2} \frac{\partial x_2 }{\partial \theta } + \frac{\partial x_3 }{\partial x_2} \frac{dx_2 }{d x_1 } \end{aligned} \end{equation}\]Putting it all together, we get:
\[\begin{equation} \begin{aligned} \frac{dx_3 }{d \theta} = ( \frac{\partial x_3 }{\partial \theta} + \frac{\partial x_3 }{\partial x_2} \frac{\partial x_2 }{\partial \theta } + \frac{\partial x_3 }{\partial x_2} \frac{dx_2 }{d x_1 } ) \end{aligned} \end{equation}\]So we see that $\frac{dx_t }{d \theta} = \sum_{1 \leq k \leq t} \frac{\partial x_t}{\partial x_k} \frac{\partial x_k}{\partial \theta }$ meaning that we need to add the derivative with respect to every latent variable before it, each multiplied by its partial derivative with respect to $\theta$. So putting it all together:
\[\begin{equation} \begin{aligned} \frac{\partial \varepsilon_t }{\partial \theta} = \frac{\partial \varepsilon_t }{\partial x_t} \frac{d x_t }{d \theta} = \sum_{1 \leq k \leq t} \underbrace{ \frac{\partial \varepsilon_t }{\partial x_t} \frac{\partial x_t}{\partial x_k}}_{\text{:=T}} \frac{\partial x_k}{\partial \theta } \end{aligned} \end{equation}\]And using the chain rule we can also write:
\[\begin{equation} \begin{aligned} \frac{\partial x_t }{\partial x_k} = \prod_{t \leq i \leq k} \frac{\partial x_i}{\partial x_{i-1}} = \prod_{t \leq i \leq k} \boldsymbol{W} diag(\sigma' (x_{i-1})) \end{aligned} \end{equation}\]Now let’s assume for simplicity that $\sigma$ is the identity function. Define $l=k-t$ and we get $\frac{\partial x_t }{\partial x_k} = W^l$
We can span $ \frac{\partial \varepsilon_t }{\partial x_t} $ using the space of the eigenvectors $W q_i = \lambda_i q_i$ from the largest eigenvector to the smallest. If we assume that W is diagonalizable, then also $W^l q_i = \lambda_i ^l q_i$ because raising a diagonalizable matrix to a power l corresponds to raising its eigenvalues to the power l. Now let’s analyze $T$:
\[\begin{equation} \begin{aligned} T = (\underbrace{\sum_{i=1}^{n} c_i q_i^T }_{ \frac{\partial \varepsilon_t }{\partial x_t}} ) W^l = \sum_{i=1}^{n} c_i (q_i^T W^l ) = \sum_{i=1}^{n} c_i q_i^T \lambda_i^l \end{aligned} \end{equation}\]Now we can see that is the biggest $\lambda$ satisfies $ \mid \lambda\mid >1$ the term will explode as $l$ becomes large. Similarly it will vanish into zero, if the magnitude of $\lambda$ is smaller than 1.
When $\sigma$ is not the identity function
If $\sigma$ is not the identity function, but rather is bounded by some constant, we can still reach the same conclusion, as described in the paper.
We assume that the nonlinearity derivative $\sigma’()$ is bounded by $\gamma$. Therefore, every element of $diag(\sigma’(x_k))$ is also bounded by $\gamma$. Let us also assume that the largest singular value of $W$ is small: $\lambda_1 < \frac{1}{\gamma}$
The 2-norm of a matrix is equal to its largest singular value, and if the matrix is diagonal it is equal to the largest absolute element on the diagonal. So, $ | diag(\sigma’(x_k)) | \leq \gamma $ and then we can write:
\[\begin{equation} \begin{aligned} \forall k, \| \frac{\partial x_{k+1}}{\partial x_{k}} \| = \underbrace{ \| \boldsymbol{W} diag(\sigma' (x_{i-1})) \| \leq \| \boldsymbol{W} \| \| diag(\sigma' (x_{i-1})) \|}_{\text{sub-multiplicative property of the matrix 2-norm}} < \underbrace{ \frac{1}{\gamma} * \gamma }_{\text{two assumptions}} < 1 \end{aligned} \end{equation}\]Let’s choose the maximum value $\eta$ such that: $ \forall k, | \frac{\partial x_{k+1}}{\partial x_{k}} | \leq \eta < 1 $
Now let’s analyze the term T again:
\[\begin{equation} \begin{aligned} \| \frac{\partial x_t }{\partial x_k} \| = \| \prod_{t \leq i \leq k} \frac{\partial x_i}{\partial x_{i-1}} \| \leq \eta ^l \end{aligned} \end{equation}\]So we can see that the norm of the Jacobian matrix goes toward 0 exponentially fast as $l$ grows, even when we use nonlinearity. $\square $