XGBoost paper explained
The final prediction for a given example is the sum of predictions from each tree.[We have k trees. T=number of leaves in a tree. w is a score from a given tree q] Loss function is a simple squared-error loss plus regularization on number of leaves and $L_2$ regularization of weight vector ($R^T$) per each tree. The total loss function cannot be differentiated, since it includes functions as parameters. Instead, the approach is a greedy algorithm, that in each step (addition of tree) minimizes the accumulated loss function which is composed of the SE loss and the regularization loss.

Then we do a Taylor-second-order expansion of the loss:

The reason we do a second order approximation, is that in the next stage when we differentiate by w, the w will remain and not disappear. Now we want to get rid of f(x) which cannot be differentiated by w, and replace it by w. If we write $I_j$ for all the instance indices that reach leaf j (this depends on the tree structure, and not the final residual weights). Then we can convert a sigma over instances, to a sigma over leaves (T) and for each leaf, iterate on all the instances that reach this leaf. It’s the same thing. Then the f() of an instance becomes the w of the leaf corresponding to this instance:
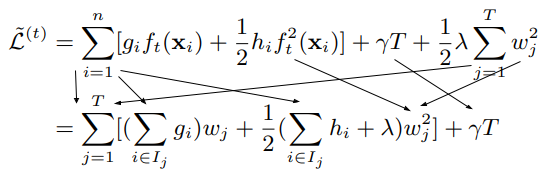
Now the equation is ready for differentiation: we just differentiate by w to get the optimal w* (meaning the optimal residuals of the leaves) for a fixed tree structure, and the corresponding optimal loss after we minimized it:
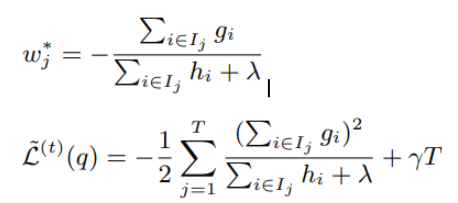
So, since for a given tree structure, we can find the optimal weights and loss, this is essentially a quality score for a tree structure, and we can check which structure is the best at each step, or to greedily start with a node, and do splits using this quality score, in the same way we use entropy in decision tree splitting. So here’s a trivial algorithm that checks all possible splits: scans all m features and all values.
